Jim, I think you were on the right track in June with your diagrams. But I don't think the question "what's the effect on BB torque from a dynamic BB position" is really the best one to ask. What we really want to know is the power split between legs and upper body when using a dynamic BB position, i.e. MBB.
In the case where the bottom bracket doesn't move, i.e. all pedaling torques
around the steer tube are instantaneously canceled by the torque from the hands on the bars, then we know the power split is 100% legs, 0% upper body. (For the upper-body portion, I'm talking about the power that is actually transferred from the upper body to the bike; if the bars don't move, the upper body can't provide any power.).
As Jim's diagrams show, when the BB does move throughout a pedal revolution, it changes the extension distance of the foot, i.e. the distance the foot moves during the leg's flexion-to-extension half-cycle. At the same time, of course, the bars move, allowing for the possibility of power input from the upper body.
What I propose is that the power split between legs and upper body is (almost?) entirely determined by the change in flexion-to-extension distance at the pedal. And we can calculate that difference; I did it graphically, below, using pieces from your earlier images, but of course the answer for any given bike will depend on the exact geometry of the bike. The first image compares stationary-BB pedal location for leg flexion (left) and leg extension (on the right). The distances are in some units chosen by my graphics program, so they don't correspond to real-world distances. But that won't affect our leg/upper-body power-split answers.
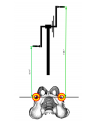
The difference between the two is 3.24" in image units. Next, measure the change in flexion and extension pedal positions when the BB moves. We'll assume the best BB movement to *shorten* the flexion-to-extension distance:

The difference between flexion and extension distances is now 3.03". Which means that by moving the BB during the half-crank-rotation for one side, the pedal moves a shorter distance by the ratio 3.03/3.24, or 93.5% of the stationary-BB distance.
And that 93.5% (again, for this chosen geometry, using Jim's original ±4.76-degree steering rotation over a full crank cycle) is the key factor in determining power split. Why?
Because of energy-balance. Let's suppose that whatever
force was provided by the foot to the pedal with a static BB is the same force used when riding with a moving BB. Same cadence, too. Not too hard to imagine. In this case, with a moving BB, the energy transferred to the drivetrain by the feet during a crank cycle is going to be 93.5% of that transferred with a static BB, because Energy = Force times Distance.
But what if we add, to the thought-experiment situation at hand, the requirement that TOTAL energy transferred to the drivetrain during a crank cycle (from the human rider) is the same, whether MBB or stationary BB? Where would the last 6.5% of the stationary-BB's energy input come from, when riding in MBB mode? Well there's only one place it *can* come from: the upper body, via the bars.
So for this particular graphically-defined geometry, the energy split per crank rev (and therefore the power split) is 14.4-to-1, legs-to-upper-body. If the force of the feet on the pedals in MBB mode is increased enough to restore the LEG power back to 100% of the LEG power for the static-BB case, then we have a brand-new 6.5% gain in power, with the source being: the upper body.
Dave





